Με ποιά ταχύτητα πρέπει να εκτοξευθεί ένα αντικείμενο ουτως ώστε να διαφύγει απο το πεδίο βαρύτητας της Γης; Και τι συμβαίνει με τις μαύρες τρύπες;
Θεωρούμε οτι η Γη δεν κινείται, δεν υπάρχουν αντιστάσεις του αέρα και οτι στο σώμα δεν ασκούνται βαρυτικές δυνάμεις απο άλλα ουράνια σώματα.
Εφόσον το βαρυτικό πεδίο της γης είναι διατρητικό θα ισχύει
Κ1+U1=K2+U2
Θα εφαρμόσουμε της σχέση αυτή για ένα σημείο πάνω στην επιφάνεια της γης και για το άπειρο. Στο άπειρο η δυναμική ενέργειά είναι μηδέν άρα U2=0. Η ελάχιστη ταχύτητα που χρειάζεται ένα σώμα για να φτάσει στο άπειρο είναι όταν K2=0. Οπότε:
Κ1+U1=0+0
Η ταχύτητα αυτή λέγεται ταχύτητα διαφυγής.
Πλανήτης
|
Ve
|
Ήλιος
|
617.5 km/s
|
Ερμής
|
4.3 km/s
|
Αφροδίτη
|
10.3 km/s
|
Γη,
|
11.2 km/s
|
Σελήνη
|
2.4 km/s
|
Άρης
|
5.0 km/s
|
Δίας
|
59.5 km/s
|
Γανυμήδης
|
2.7 km/s
|
Κρόνος
|
35.6 km/s
|
Ουρανός
|
21.2 km/s
|
Ποσειδώνας
|
23.6 km/s
|
Πλούτων
|
1.2 km/s
|
Ας δούμε την ταχύτητα διαφυγής με άλλο τρόπο. Ας βρούμε τι ακτίνα πρέπει να έχει ένα ουράνιο σώμα ούτως ώστε να μην μπορεί να διαφύγει απο την επιφάνειά του.
Η μεγαλύτερη ταχύτητα στον κόσμο είναι αυτής του φωτός. c=3*10^8 m/s
γνωστή και ώς Schwarzschild ακτίνα (Schwarzschild radius). Ένα ουράνιο σώμα αν συμπιεστεί και έχει ακτίνα ίση απο την Schwarzschild ακτίνα τότε η ταχύτητα διαφυγής στην επιφάνεια θα ισούται με την ταχύτητα του φωτός. Αν η ακτίνα είναι μικρότερη τότε δεν θα επιτρέπει να διαφεύγει τίποτε, ούτε καν το φως. Τέτοια σώματα στην σύγχρονη φυσική χαρακτηρίζονται ως μαύρες τρύπες. Η Γή για παράδειγμα θα πρέπει να συμπιεστεί και να έχει ακτίνα 9.0 mm όσο ενα φιστίκι για να γίνει μαύρη τρύπα πράγμα που είναι αδύνατον στην πραγματικότητα.
Τι θα συμβεί να πέσει κάποιος σε μια μαύρη τρύπα;
Καθώς θα πέφτει κάποιος σε μια μαύρη τρύπα η ταχύτητα θα μεγαλώνει όλο και περισσότερο λόγω της βαρύτητας. Επειδή τα πόδια είναι πιο κοντά σε σχέση με τα χέρια και το κεφάλι το σώμα θα αρχίσει να τεντώνεται. Όσο πιο μικρή είναι μια μαύρη τρύπα τόσο πιο ισχυρή θα είναι και οι παλιρροιακές δυνάμεις.
Για τις απλές μαύρες τρύπες μερικών ηλιακών μαζών, στην πραγματικότητα υπάρχουν μεγάλες
παλιρροιακές δυνάμεις και έξω από τον ορίζοντα γεγονότων, οπότε πιθανότατα δεν
θα υπάρχει περίπτωση να είστε στην τρύπα ζωντανοί και μη τεντωμένοι. Για μια μαύρη τρύπα
των 8 ηλιακών μαζών, για παράδειγμα, η τιμή του r στην οποία παλίρροιες να αποβεί μοιραία είναι
περίπου 400 χιλιόμετρα, και η ακτίνα Schwarzschild είναι μόλις 24 χιλιόμετρα. Αλλά παλιρροϊκή τάσεις
είναι ανάλογη με M/r3. Ως εκ τούτου το μοιραίο r πηγαίνει ως κυβική ρίζα της μάζας, ενώ η
ακτίνα Schwarzschild της
μαύρης τρύπας είναι ανάλογη προς τη μάζα. Έτσι, για τις μαύρες τρύπες
μεγαλύτερες από περίπου 1000 ηλιακές μάζες θα μπορούσε πιθανώς να πέσετε και να είστε ζωντανοί, και για ακόμη μεγαλύτερες αυτά που μπορεί να μην παρατηρήσετε ακόμη
και τις παλιρροϊκές δυνάμεις μέχρι να είστε μέσα στον ορίζοντα και να είστε καταδικασμένοι.
Πηγές:
http://math.ucr.edu/home/baez/physics/Relativity/BlackHoles/fall_in.html
http://hubblesite.org/explore_astronomy/black_holes/encyc_mod3_q16.html
http://hyperphysics.phy-astr.gsu.edu/hbase/astro/blkhol.html
http://en.wikipedia.org/wiki/Schwarzschild_radius
http://en.wikipedia.org/wiki/Escape_velocity
Πηγές:
http://math.ucr.edu/home/baez/physics/Relativity/BlackHoles/fall_in.html
http://hubblesite.org/explore_astronomy/black_holes/encyc_mod3_q16.html
http://hyperphysics.phy-astr.gsu.edu/hbase/astro/blkhol.html
http://en.wikipedia.org/wiki/Schwarzschild_radius
http://en.wikipedia.org/wiki/Escape_velocity

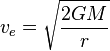
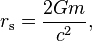


Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου